Краеугольным камнем знания секретных школ мистерий, связанного со скрытым порядком во Вселенной, всегда была сакральная геометрия.
Сакральная геометрия – это просто еще одна форма вибрации или “кристаллизованной” музыки. Рассмотрим следующий пример:
Сначала мы дергаем гитарную струну. Это создает “стоячие волны”, то есть волны, не движущиеся по струне назад и вперед, а остающиеся на одном месте. Мы увидим места, где имеется сильное вертикальное движение, представляющее собой верх и низ волны, и другие места, где вертикального движения нет. Такие места называются узлами.
Узлы, формирующиеся в любом виде стоячей волны, всегда будут расположены на одинаковом расстоянии друг от друга, а скорость вибрации будет определять количество появляющихся узлов. Это значит: чем выше вибрация, тем больше узлов.
В двух измерениях мы можем воспользоваться осциллографом или подвергнуть вибрации плоскую круглую “пластину Хладни” и наблюдать появление узлов, формирующих простые геометрические формы, такие как квадрат, треугольник и шестиугольник. Такая работа повторялась много раз д-ром Гансом Йенни, Джеральдом Хокинсом и другими.
• Если окружность имеет три узла, расположенных на одинаковом расстоянии друг от друга, при их соединении получится треугольник.
• Если окружность имеет четыре узла, образуется квадрат.
• Если окружность имеет пять узлов, образуется пятиугольник.
• Шесть узлов образуют шестиугольник, и так далее.
Хотя в терминах волновой механики это очень простая концепция, Джеральд Хокинс первым математически доказал, что вписанные в окружности геометрии являются музыкальными отношениями. Мы, конечно, удивимся, узнав, что к этому открытию его привел анализ разных геометрических образований “кругов на полях”, которые появлялись буквально за одну ночь на полях английской сельской местности. Это описывались в обеих предыдущих книгах.
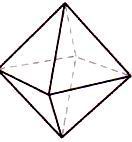
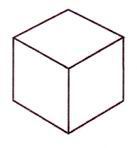
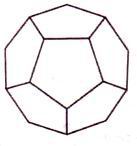
Самые глубинные и самые уважаемые формы сакральной геометрии трехмерны и известны как Платоновы Твердые Тела. Имеется лишь пять форм, удовлетворяющих всем необходимым правилам. Это восьмигранный октаэдр, четырехгранный тетраэдр, шестигранный куб, двенадцатигранный додекаэдр и двадцатигранный икосаэдр.
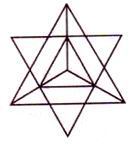
На нижеприведенном рисунке тетраэдр изображен в виде “звездного тетраэдра” или сплетенного тетраэдра, что означает два тетраэдра, соединенных вместе в совершенной симметрии.
 |
 |
 |
 |
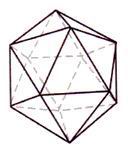 |
| Октаэдр | Звездный тетраэдр | Куб | Додекаэдр | Икосаэдр |
Рис. 3.1 - Пять Платоновых Твердых Тел
Вот некоторые основные правила этих геометрических твердых тел:
• Каждая грань геометрического тела будет иметь одинаковую форму:
◦ октаэдр, тетраэдр и икосаэдр - равнобедренные треугольники,
◦ куб – квадраты,
◦ додекаэдр – пятиугольники.
• Каждое ребро каждой формы будет одинаковой длины.
• Все внутренние углы каждой формы равны между собой.
И самое важное:
• Каждая форма будет совершенно вписываться в сферу, и все вершины будут касаться сферы, не перекрывая друг друга.
Подобно двумерным фигурам, включающим треугольник, квадрат, пятиугольник и шестиугольник внутри окружности, Платоновы Твердые Тела – это представления волновых форм в трех измерениях. Это положение нельзя недооценивать. Каждая вершина Платоновых Твердых Тел касается сферы в том месте, где вибрации сводятся на нет, образуя узел. Следовательно, то, что мы видим, - это трехмерное геометрическое изображение вибрации/пульсации.
И студенты Бакминстера Фуллера, и его протеже д-р Ганс Йенни придумали умные эксперименты, показавшие, что внутри вибрирующей/пульсирующей сферы будут формироваться Платоновы Твердые Тела.
В эксперименте, проведенном студентами Фуллера, сферический, воздушный шар помещался в чернила и пульсировал на “чистых” звуковых частотах, известных как диатонические звуковые отношения.
На поверхности сферы образовывалось небольшое количество равноудаленных узлов и тонкие линии, соединяющие узлы друг с другом. Если будет четыре равно распределенных узла, вы увидите тетраэдр. Шесть равно распределенных узлов дадут октаэдр. Восемь равно распределенных узлов дадут куб. Двадцать равно распределенных узлов дадут додекаэдр, а двенадцать – икосаэдр.
Прямые линии, которые мы видим на этих геометрических объектах, представляют напряжения, создающиеся “кратчайшим расстоянием между двумя точками” для каждого из узлов, поскольку они распределяются по всей поверхности сферы..

Рис. 3.2 – Д-р Ганс Йенни: образование Платоновых Твердых Тел в сферической вибрирующей жидкости
Д-р Ганс Йенни провел аналогичный эксперимент (небольшая часть которого приведена на рис 3.2) с каплей воды, содержащей слегка окрашенные частицы, что известно как “коллоидная взвесь”.
Когда почти сферическая капля взвеси вибрировала на разных “диатонических” музыкальных частотах, внутри нее появлялись Платоновы Тела, окруженные эллиптическими кривыми линиями, соединяющими узлы. На вышеприведенном рисунке в центральной области явно видны два тетраэдра. Если бы капля была совершенной, а не сплющенной сферой, образования были бы видны еще яснее.
ПЛАТОНОВЫ ТВЕРДЫЕ ТЕЛА И “СИММЕТРИЯ” В ФИЗИКЕ
Секрет и значение Платоновых Твердых Тел не совсем утеряны в современной науке, поскольку эти формы удовлетворяют всем необходимым критериям для создания “симметрии” в физике многими разными способами.
По этой причине они часто появляются в теориях, имеющих дело с многомерностью, когда множество “планов” должно симметрично пересекаться так, чтобы их можно было по-разному поворачивать, и чтобы они всегда оставались в одних и тех же положениях относительно друг друга. Такие теории многомерности включают “теорию групп”, известную и как “калибровочная теория”, которая последовательно пользуется разными Платоновыми моделями для “свернутого” гипермерного пространства.
Считается, что “модулярные функции” – это самый продвинутый математический инструментарий, пригодный для изучения и понимания “более высоких измерений”, на них целиком и полностью построена теория Суперструн.
Уже известно, что Платоновы Твердые Тела – это мастер ключ к открытию мира “более высоких измерений”. Помните, что мы упомянули вышеуказанные положения очень кратко, поскольку они детально рассматривались в предыдущих книгах, и ключ – это симметрия.
Если мы вспомним о симметрических качествах Платоновых Тел, тогда слова д-ра Вольфа из главы 5, озаглавленной О важности жизни в трех измерениях, обретают весомый смысл:
Стр. 71 - “В качестве вашего наставника в исследовании, могу сказать: “Когда бы вы ни столкнулись с ситуацией симметрии в физике, остановитесь и подумайте! Потому что, воспользовавшись свойством симметрии, вы всегда будете находить более легкий способ решения проблемы. Это одна из наград в игре с симметрией. Идеи ясны…
В математике и геометрии требуется точность; поэтому именно симметрия определяет, что функция или геометрическая фигура остается неизменной, несмотря на: 1) поворот координат; 2) движение по оси и 3) замену переменных.
В физической науке, которая нас интересует, наличие симметрии обычно означает, что закон Природы не меняется, несмотря на: 1)поворот координат в пространстве; 2) движение по оси в пространстве; 3) замену прошлого на будущее так, что t становится –t; 4) взаимную замену двух координат, такую как замену x на y, z на –z и так далее; 5) замену любой данной переменной”.
Из всех имеющихся форм Платоновы Твердые Тела обладают самой совершенной симметрией, хотя здесь д-р Вольф не называет их по именам. В следующем отрывке из работы д-ра Аспдена автор называет формирующиеся в эфире Платоновы Твердые Тела “жидкими кристаллами” и объясняет, почему они обладают поведением твердых тел, даже появляясь в жидкообразной среде:
“Физики 19-го века ломали голову над эфиром потому, что он демонстрирует как свойства жидкости, так и твердого тела. Таким его воспринимали с того времени, когда о “жидких кристаллах” было известно очень мало, если вообще было известно.
Дисплеи многих карманных калькуляторов пользуются электрическими сигналами и основаны на свойствах вещества, которое, подобно эфиру, демонстрирует свойства, как жидкости, так и твердого тела как функцию нарушений электрического поля.
Это убедительно объясняет, почему Тесла утверждал, что для материи эфир ведет себя как жидкость, а для света и тепла - как твердое тело. Платоновы Твердые Тела действительно ведут себя так, как будто являются структурными каркасами в эфире, организующими энергетические потоки в особые паттерны.
Отсюда, Платоновы Твердые Тела – это простые геометрические формы “кристаллизованной музыки”, естественно формирующиеся в пульсирующем эфире. Следует помнить еще одно важное положение: поскольку иерархия Платоновых Твердых Тел “растет” друг в друге, движение всегда будет происходить по спиралям, в основном в классическом отношении “φ”.
Видно, что торсионные волны тоже следуют паттерну “φ”. Мы будем исследовать это подробнее в главе 9, когда будем обсуждать недооцененный феномен “силы пирамид” и “эффект полостных структур”, который первым обнаружил д-р Виктор Гребенников.
http://www.divinecosmos.e-puzzle.ru/3Chapter3.htm
